Mathématiques élémentaires

Taper des maths

Dans le texte

Méthodes

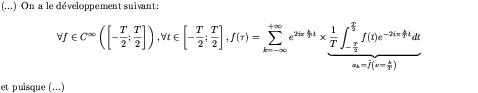
Pour taper des maths dans le texte, on place le contenu de la formule entre deux symboles « $ ». Par exemple:

(...) on y verra la démonstration que $2 + 2 = 4$ (...)

Remarque importante concernant la lisibilité: les espaces ne comptent pas pour le contenu des mathématiques et $2+2=4$ a rigoureusement le même effet que $2 + 2 = 4$. L'avantage de la seconde écriture est qu'elle est notablement plus lisible surtout quand les formules deviennent complexes.

Remarques concernant la typographie: il est à noter que les modes mathématiques peuvent être utiles en d'autres circonstances que l'écriture de formule mathématiques.

Les variables physiques devront être typographiées de manière cohérente, on notera donc systématiquement $T$ la température qui aura donc la même typographie que dans les formules comme $PV = n RT$. Si l'on souhaite en physique avoir des variables droites (et non italiques) on peut utiliser la commande $\mathrm{T}$ ou un changement de \mathcode.

Pour obtenir le signe « moins », il faut taper $-1$ (observer la différence entre - [tiret], $-$ [signe « moins »], -- [intervalle comme dans 1939--1945] et --- [incise]).

Enfin, on notera que $lettre$ est le produit de quatre variables l, e (deux fois), t (deux fois) et r. Pour des noms complexes dans les formules on pourra utiliser $\mathit{mot}$ pour un mot en italique (observer la différence entre $efficace$ et $\mathit{efficace}$) ou $\mathrm{mot}$ pour un mot en police droite ou encore la commande $\text{...}$ du package amsmath. L'important est d'avoir une démarche cohérente avant tout.

Une autre possibilité est d'utiliser \(contenu de la formule\) ou encore l'environnement math. Exemple: 

(...) d'après certaines personnes \(2 + 2 = 5\) mais d'autres affirment
      également que \begin{math}2 - 1 = 0\end{math}.  La réalité est tout
      autre (...)

Comment empêcher LaTeX de couper mes formules

(La)TeX s'autorise à couper une formule dans le texte au niveau des opérations (comme +, *) et des relations (comme =, <). On peut interdire la coupure à des endroits précis de la formule grâce aux accolades { et }. Tout ce qui dans une formule dans le texte (cela ne s'applique pas au texte normal, ni aux formules centrées) et entre accolades ne sera pas coupé. Ainsi dans

(...) texte $f(x, y) = {x + y}$ texte (...)

la césure ne peut intervenir qu'après le = (tandis que sans les accolades, la césure aurait tout aussi bien pu avoir lieu après le +). Cette méthode a le mérite de la simplicité, mais elle présente également un inconvénient qu'on pourra négliger à moins d'être perfectionniste : les espaces entre les accolades ne sont pas capables de s'étirer.

Si l'on souhaite empêcher la césure dans toute formule écrite dans un paragraphe (globalement dans tout le document), on peut mettre dans son préambule (avant le \begin{document}):

\relpenalty=10000
\binoppenalty=10000

En effet, LaTeX ne s'autorise à couper une formule qu'au niveau des relations (=, <, etc.) ou des opérations binaires (+, -, etc.). Si une telle coupure intervient, elle s'accompagne d'une pénalité. Si cette pénalité est trop forte, le point de coupure sera évité. Les valeurs présentées juste au-dessus sont des pénalités infinies pour (La)TeX.

Cependant cette méthode est déconseillée, car elle va gêner LaTeX dans son mécanisme de formation des paragraphes et l'on risque de nombreux warnings: Underfull hbox et Overfull hbox. Il convient de se demander si une formule donnée n'aurait pas plutôt sa place dans un display (formule centrée sur une ligne à part) qui est le sujet dont nous allons traiter un peu plus bas.

Comment dire à LaTeX de couper mes formules

Si, au contraire, on souhaite que LaTeX puisse couper à un endroit on rajoutera un \linebreak (qui suggère un point de coupure mais ne le force pas obligatoirement). Ce point de coupure n'a pas à être accompagné de relation ou d'opérateur binaires.

(...) texte ${coupera pas + coupera pas + coupera pas + coupera pas +
      coupera pas + coupera}\linebreak[1]{pas + coupera pas}$ (...)

L'argument optionnel de \linebreak spécifie l'insistance de la requête (4, la valeur par défaut, force la coupure) ; ici, la valeur 1 signifie « si tu peux couper ici c'est plutôt sympa ».

Formule « displayée »

Centrer une équation

Une formule importante ou assez grande peut être mise, centrée, sur une ligne à part. Pour ce faire, elle doit être tapée soit entre \[ et \], soit entre \begin{displaymath} et \end{displaymath}. Exemple: 

(...) On a le développement suivant:
\[ \forall f\in C^\infty\left(\left[-\frac{T}{2};\frac{T}{2}\right]\right),
   \forall t\in \left[-\frac{T}{2};\frac{T}{2}\right],
   f(\tau) = \sum_{k = -\infty}^{+\infty} e^{2i\pi\frac{k}{T}t} \times
   \underbrace{\frac{1}{T}
               \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) e^{-2i\pi\frac{k}{T}t} dt
              }_{a_k = \tilde{f}\left(\nu = \frac{k}{T}\right)}
\]
et puisque (...)

ce qui donne le résultat suivant

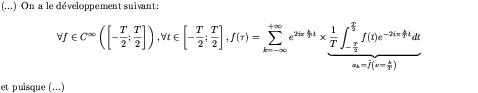
Exemple grande formule

Pour aérer on peut commenter une ligne avant et une ligne avant la formule (et profiter du fait les espaces sont ignorées en mode mathématique pour réarranger la formule)... ainsi :

(...)
On a le développement suivant:
%%
\[ \forall f \in C^\infty
   \left( \left[ -\frac{T}{2} ; \frac{T}{2} \right] \right),
   %%
   \forall t \in \left[ -\frac{T}{2} ; \frac{T}{2} \right],
   %%
   f(\tau) = \sum_{k = -\infty}^{+\infty}
             e^{2i\pi\frac{k}{T}t} \times
             \underbrace{
                 \frac{1}{T}
                 \int_{-\frac{T}{2}}^{\frac{T}{2}
                      f(t) e^{-2i\pi\frac{k}{T}t} dt
             }_{a_k = \tilde{f}\left(\nu = \frac{k}{T}\right)}
\]
%%
et puisque
(...)

est plus lisible, non? Pensez que la lisibilité permettra de corriger plus facilement des erreurs et rendra le document source moins confus.

N'omettez pas les commentaires, ne mettez pas de ligne blanche avant et après les commandes \[ et \] (sauf si vous voulez réellement commencer un nouveau paragraphe avec une formule displayée — ce qui n'est pas conseillé par les typographes), les lignes blanches ne sont pas anodines en LaTeX.

N'utilisez pas $$...$$ qui est une construction de plain TeX qui génère un espacement incorrect du document et n'honore pas les options de classe dont nous allons parler plus loin. Cette forme est à bannir.

Numéroter ses équations

On peut numéroter les formules. Cela se fait tout naturellement avec l'environnement equation remplaçant \[...\] (ou \begin{displaymath}...\end{displaymath}). Cet environnement offre la possiblité d'utiliser les foncionnalités de \label, \ref et \pageref.

Einstein a établi la célèbre formule~\ref{eq-Einstein}.
%%
\begin{equation}
  \label{eq-Einstein}
  E = mc^2
\end{equation}

donne

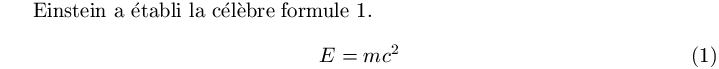
Exemple équation

Options des classes standard

On peut passer aux classes standard article, book, report les options suivantes, qui modifient l'aspect des équations numérotées (c'est-à-dire entrées avec l'environnement equation) et les formules displayée simples :

option
leqno
option leqno
option
fleqn
option fleqn
options
fleqn et
leqno
options leqno et fleqn

Le paramètre qui règle l'indentation de l'option fleqn est la longueur \mathindent qu'on peut modifier à l'aide de \setlength.

Ma formule est trop grande

La formule est trop grande pour entrer dans un displaymath et les commandes \linebreak, \\ ou \par ne fonctionnent pas. Utilisez les environnements du package amsmath (ou trouver la documentation du package amsmath ?), multline par exemple.

Symboles, commandes et cie

Nota Bene : nous omettrons de préciser que les codes précisés ici sont à taper en mode math.

Le commencement

\frac{a}{b} \frac{a}{b}
\sqrt{abcd} \sqrt{abcd}
\sqrt[n]{abcd} \sqrt[n]{abcd}

Les symboles

Symboles divers. 
\forall \exists
  \infty \partial
\forall \exists \infty \partial 
\cdots \ldots
  \vdots \ddots
\cdots \ldots \vdots \ddots

La différence entre \ldots et \cdots est que ces derniers sont centrés verticalement alors que \ldots sont au niveau de la base de la ligne (ce qui ne se voit pas dans le tableau). La typographie veut qu'on utilise $a, \ldots, b$ et $a + \cdots + b$, donc selon le type de symboles dont la répétition est représentée par les points.

Accents en mode mathématique

Les accents utilisés usuellement dans le texte (\', etc.), ne fonctionnent pas en mode mathématique. On peut les obtenir avec des commandes spécifiques.

Accents. 
\hat{a} \check{a}
  \acute{a} \grave{a}
\hat \check \acute \grave 
\bar{a} \vec{a}
  \dot{a} \ddot{a}
\bar \vec \dot \ddot 
\breve{a} \tilde{a}
  \mathring{a}
\breve \tilde \mathring

Lettres grecques

Lettres grecques. 
\alpha \beta  \gamma   \delta \epsilon \varepsilon
\zeta  \eta   \theta   \iota  \kappa   \lambda
\mu    \nu    \xi      \pi    \varrho  \rho
\sigma \tau   \upsilon \phi   \varphi  \chi
\psi   \omega \Gamma   \Delta \Theta   \Lambda
\Xi    \Pi    \Upsilon \Phi   \Psi     \Omega
Lettres grecques

Opérateurs binaires

Opérateurs binaires. 
\pm \times \div \cdot
\pm \times \div \cdot 
\circ \bullet \oplus \otimes
\circ \bullet \oplus \otimes 
\cap \cup \vee \wedge
\cap \cup \vee \wedge

Grands opérateurs

Les « grands opérateurs » sont listés dans la table suivante.

Grands opérateurs.
\sum_{0}^{\infty} \sum \int_{0}^{\infty} \int \prod_{0}^{\infty} \prod
\bigcap_{0}^{\infty} \bigcap \bigcup_{0}^{\infty} \bigcup

On notera la différence de rendu de ces opérateurs selon qu'ils sont en mode math (entre $ ... $) ou en mode displaymath (entre \[ ... \]). Ainsi pour l'opérateur \sum:

\sum_{0}^{\infty} en mode math textstyle \sum
\sum_{0}^{\infty} en mode displaymath displaystyle \sum

Cela permet de garder un interligne fixe.

Les relations

Relations binaires. 
\propto \approx \sim \simeq
\propto \approx \sim \simeq 
\subseteq \supseteq \in \equiv
\subseteq \supseteq \in \equiv 
\rightarrow \Rightarrow
\leftarrow \Leftarrow
\rightarrow \Rightarrow \leftarrow \Leftarrow 
\leftrightarrow \Leftrightarrow
\longleftrightarrow \Longleftrightarrow
\leftrightarrow \Leftrightarrow \longleftrightarrow \Longleftrightarrow

La négation d'une relation peut être obtenue en la précédant de \not. Par exemple la relation «n'appartient pas à» peut s'écrire \not\in.

Les délimiteurs

Les délimiteurs sont les parenthèses au sens large (accolades, barres de valeur absolue, etc.).

Les Délimiteurs.
()[]\{\}\langle\rangle ()[]\{\}\langle\rangle
\uparrow\downarrow\updownarrow
\Uparrow\Downarrow \Updownarrow		 \uparrow\downarrow\updownarrow\Uparrow\Downarrow \Updownarrow
\lfloor\rfloor\lceil\rceil
/ \backslash | \|		 \lfloor\rfloor\lceil\rceil / \backslash | \|

Les tailles peuvent être modifiées soit à la main:

Les tailles de délimiteurs.
(\big(\Big(\bigg(\Bigg( \big \Big \bigg \Bigg

soit automatiquement à l'aide \left et \right. On doit avoir systématiquement un \left pour un \right dans la même formule. La partie de la formule comprise entre \left et \right définit par sa hauteur la taille des délimiteurs qui sont précisés ainsi:

\left<delim1> <formule> \right<delim2>

delim1 et delim2 n'ont aucune raison d'être identiques. Un «.» est un délimiteur dans un contexte de \left ou \right et signifie «pas de délimiteur» mais permet de focaliser l'action de \left et \right sur une partie de la formule. 

\[
  |x| = \left\{
          \begin{array}{ll}
            +x & \qquad \mathrm{si}\quad x\geq 0 \\
            -x & \qquad \mathrm{sinon} \\
          \end{array}
        \right.
\]

donne le résultat suivant

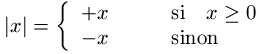
cases

Nota Bene: l'environnement array est l'équivalent en mode mathématique de l'environnement tabular. Pour son utilisation, on se reportera donc à la page concernant tabular.

Les fonctions

Pour taper la fonction sinus, on ne peut pas utiliser $sin(x)$ dont le résultat est le produit de s, i et n(x). En outre, traditionnellement les fonctions sont en police droite. La première idée est d'utiliser $\mathrm{sin}(x)$ qui a la tête voulue. Cependant \mathrm{sin} ne se comporte pas comme une fonction. Comparer:

Les tailles de délimiteurs.
\[ abc \mathrm{sin}(x)
  \qquad abc\sin(x) \]		 opérateur sinus

Les fonctions prédéfinies sont: \sin, \cos, \tan, \arcsin, \arccos, \arctan, \sinh, \cosh, \tanh, \cot, \log, \ln, \lim. Pour en définir d'autres utiliser les commandes \DeclareMathOperator et \DeclareMathOperator* du package amsmath.

Espacement

Il est parfois nécessaire d'ajuster l'espacement d'une formule à la main ((La)TeX ne peut pas tout faire tout seul). Par exemple, dans une intégrale, pour séparer la fonction intégrée de «dx». Pour cela, on dispose de:

Aller plus loin

Recherche de symboles. Une liste de (presque) tous les symboles accessibles avec LaTeX est maintenue à jour sur le CTAN, les fichiers symbols-*.* disponibles à l'adresse http://www.ctan.org/tex-archive/info/symbols/comprehensive/.

Pour des maths sophistiquées, il est quasiment indispensable de charger le package amsmath qui (re)définit de nombreux environnements très utiles. Cette page web ne peut prétendre couvrir toutes les ressources disponibles concernant les mathématiques avec LaTeX, heureusement la documentation de amsmath est très complète et facile d'accès, nous vous renvoyons vers cette documentation: le fichier amsldoc.dvi que vous pourrez trouver soit sur votre distribution LaTeX (essayer la commande texdoc amsldoc) soit sur internet (google avec le mot-clef «amsldoc.dvi» permet de trouver en une dizaine de secondes).

Auteur : Josselin Noirel.